Chapter 4 Videos: Differential Equations (Continuity and the Navier-Stokes Equations)

Part 1: Differential Relations for Fluid Flow (20:23)
Introduction to Chapter 4. The Continuity and Navier-Stokes equations are presented and briefly discussed. Exact solutions and the CFD applications of these equations are briefly discussed.
YouTube Video
Introduction to Chapter 4. The Continuity and Navier-Stokes equations are presented and briefly discussed. Exact solutions and the CFD applications of these equations are briefly discussed.
YouTube Video
| Chapter 4 Part 1 (pdf) | |
| File Size: | 754 kb |
| File Type: | |
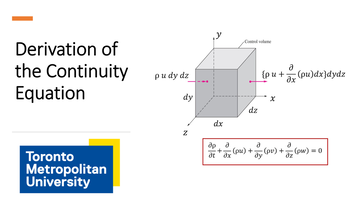
Part 2: Differential Relations for Fluid Flow (18:35)
Derivation of the general continuity equation for three dimensional unsteady incompressible flow. Vector notation and cylindrical coordinates are also discussed. A numerical example is also presented.
YouTube Video
Derivation of the general continuity equation for three dimensional unsteady incompressible flow. Vector notation and cylindrical coordinates are also discussed. A numerical example is also presented.
YouTube Video
| Chapter 4 Part 2 (pdf) | |
| File Size: | 1295 kb |
| File Type: | |

Part 3: Differential Relations for Fluid Flow (27:41)
Derivation of the fluid acceleration field. The difference between local acceleration and convective acceleration is discussed in some detail. Two mathematical example problems are also presented.
YouTube Video
Derivation of the fluid acceleration field. The difference between local acceleration and convective acceleration is discussed in some detail. Two mathematical example problems are also presented.
YouTube Video
| Chapter 4 Part 3 (pdf) | |
| File Size: | 1244 kb |
| File Type: | |

Part 4: Differential Relations for Fluid Flow (31:49)
Derivation of the Navier-Stokes equations, the differential equations for conservation of momentum in fluid flow. Euler's equation for inviscid flow is also briefly discussed. A sample problem that involves showing that a given velocity vector field satisfies the Navier-Stokes equations.
YouTube Video
Derivation of the Navier-Stokes equations, the differential equations for conservation of momentum in fluid flow. Euler's equation for inviscid flow is also briefly discussed. A sample problem that involves showing that a given velocity vector field satisfies the Navier-Stokes equations.
YouTube Video
| Chapter 4 Part 4 (pdf) | |
| File Size: | 2125 kb |
| File Type: | |

Part 5: Differential Relations for Fluid Flow (21:12)
Two exact solutions to the incompressible continuity and Navier-Stokes equations. One solution is for laminar steady flow between fixed parallel plates, where the flow is driven by a pressure gradient (Poiseuille Flow). The other solution is for laminar steady flow between parallel plates where the flow is driven only by the motion of the upper plate (Couette Flow).
YouTube Video
Two exact solutions to the incompressible continuity and Navier-Stokes equations. One solution is for laminar steady flow between fixed parallel plates, where the flow is driven by a pressure gradient (Poiseuille Flow). The other solution is for laminar steady flow between parallel plates where the flow is driven only by the motion of the upper plate (Couette Flow).
YouTube Video
| Chapter 4 Part 5 (pdf) | |
| File Size: | 1271 kb |
| File Type: | |

Part 6: Differential Relations for Fluid Flow (21:28)
The exact solution of the Navier-Stokes and Continuity equations for fully developed laminar flow in a round pipe (Hagen-Poiseuille Flow). The video concludes with a numerical example.
YouTube Video
The exact solution of the Navier-Stokes and Continuity equations for fully developed laminar flow in a round pipe (Hagen-Poiseuille Flow). The video concludes with a numerical example.
YouTube Video
| Chapter 4 Part 6 (pdf) | |
| File Size: | 513 kb |
| File Type: | |
An Additional Solved Navier-Stokes Problem

Solved Exam Problem: Navier-Stokes Solution (12:39)
An additional solved problem for study purposes. A final exam question (Fall 2022) on solving the Navier-Stokes equations. The velocity and pressure fields are calculated for a gravity-driven liquid film on an inclined plate. The no-shear stress boundary condition at the top of the liquid film is also discussed.
YouTube Video
An additional solved problem for study purposes. A final exam question (Fall 2022) on solving the Navier-Stokes equations. The velocity and pressure fields are calculated for a gravity-driven liquid film on an inclined plate. The no-shear stress boundary condition at the top of the liquid film is also discussed.
YouTube Video
| Navier-Stokes Solution. Final Exam Question (pdf) | |
| File Size: | 1224 kb |
| File Type: | |
Toronto Metropolitan University


